Hi, hier chemweazle,
Berechnen Sie die Partialdrücke, Partialdichten und Volumenarbeit
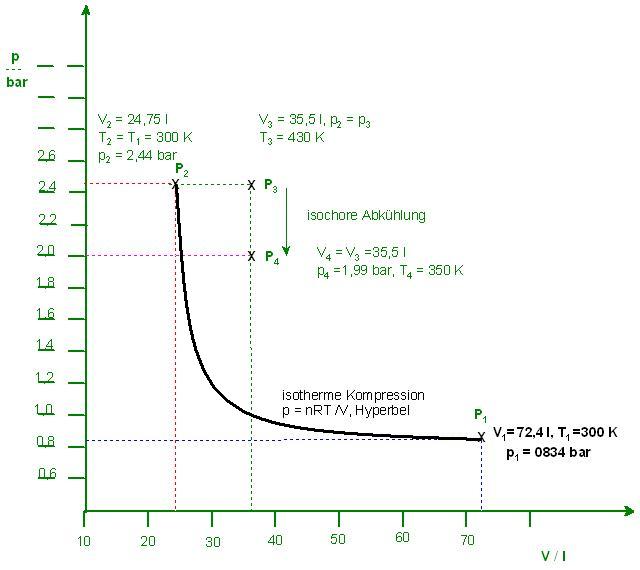
Tragen Sie die Zustandsänderungen in ein p-V-Diagramm ein. Berechnen Sie die Partialdrücke
pi und die Partialdichten ρi der Komponenten im Zustand IV und die reversible Volumenarbeit
wrev für den Prozess A.
Ein System bestehend aus Stickstoff (80 mol-%) und Sauerstoff, das geschlossen, gasförmig
x(N2) = 0,8 = 4⁄5, x(O2) = ( 1 - 0,8 ) = 0,2 = 1⁄5
vorliegt und sich wie ein ideales Gas verhält, liegt in einem Zustand I bei 0,834 bar und 300 K mit einem Volumen von 72,4 L vor. Es durchläuft folgende Prozesse: Anfangszustand, Zustand 1
p1 = 0,834 bar = 83400 Pa = 83400 N /m2, V1 = 72,4 l = 0,0724 m3 und T1 = 300 K
Die Gesamtstoffmenge des idealen Gasgemisches n:
n = n(N2) + n(O2)
$$n = \frac{p\cdot V}{RT}$$
$$n = \frac{83400\cdot N\cdot 0,0724\cdot m^{3}\cdot K\cdot mol}{m^{2}\cdot 8,314\cdot N\cdot m\cdot 300\cdot K}$$
n = 2,4208804426268943949963916285783 mol ≈ 2,421 mol
Zustand 2
A) aus dem Zustand I isotherm in den Zustand II (pII = 2,44 bar), Zustand 2
Isotherme, reversible Kompression des idealen Gases, hierbei wird dem System Druckvolumarbeit zugeführt und da die Temperatur konstant bleibt, muß das System Wärme an die Umgebung abgeben.
T = const. = 300 K
Das Volumen ist nach der Kompression, V2 kleiner als das Ausgangsvolumen, V1
Der Druck am Ende, im Zustand 2, ist größer als der Druck am Anfangszustand. Die Drücke verhalten sich umgekehrt wie die Volumina.
$$\frac{p_{2}}{p_{1}} = \frac{V_{1}}{V_{2}}$$
p2 = 2,44 bar und p1 = 0,834 bar
$$w_{rev} = - nRT\cdot \int\limits_ {V_{1}}^{V_{2}}\cdot \frac{dV}{V}$$
V2 < V1
Das Volumen im Zustand 2, nach der Kompression:
$$\frac{p_{2}}{p_{1}} = \frac{2,44\cdot bar}{0,834\cdot bar} = 2,9256594724220623501199040767386 \approx 2,9257$$
$$\frac{V_{1}}{V_{2}} = \frac{p_{2}}{p_{1}} = 2,9257$$
$$V_{2} = \frac{V_{1}}{2,9257} = \frac{72,4\cdot l}{2,9257} \approx 24,746\cdot l = 0,024746 m^{3}$$
bzw.
$$\frac{V_{2}}{V_{1}} = \frac{1}{2,9257}$$
$$w_{rev} = - nRT\cdot ln\left(\frac{V_{2}}{V_{1}}\right)$$
$$ln\left(\frac{V_{2}}{V_{1}}\right) = ln( 1) - ln( 2,9257 ) = 0 - ln( 2,9257 ) = - ln( 2,9257 ) \approx - 1,0735$$
wrev = 2,421 mol * 8,314 ( J / K * mol ) * 300 K * 1,0735 ≈6482,285 J
Zustand 3
B) dann isobar in den Zustand III (TIII = 430 K), anschließend
Es wird Wärme dem System zugeführt bei constantem Druck, also wird vom System Volumarbeit an die Umgebung auch abgegeben.
ΔH = n* Cp,m * ΔT, T1 = T2 = 300K und T3 = 430 K
⇒ ΔT = T3 - T1 = ( 430 -300 ) K = 130 K
Nun fehlt die Wärmekapazität für diese Gasmischung. Diese besteht aus linearen Molekülen Stickstoff und Sauerstoff. Es kommen neben den drei Translationsfreiheitsgraden( 3/2 R ) plus R für die Volumarbeit gegen den konst. Atmosphärendruck, bis jetzt 5 /2 R, plus evtl. 2 Rotationsfreiheitsgrade( 2 /2 R).
Also alle Freiheitsgrade ohne Berücksichtigung der Molekülschwingungen ergeben dann für 1 mol ideales Gas die molare Wärmekapazität bei konstantem Druck, von: Cp,m = (7⁄2) * R.
Cp,m = 7⁄2 R
$$\Delta H = n\cdot \frac{7}{2}\cdot R\cdot \Delta T$$
$$\Delta H = 2,421\cdot mol\cdot \frac{7}{2}\cdot \frac{8,314\cdot J\cdot 130\cdot K}{K\cdot mol}$$
ΔH = 2,421 * 3,5 * 8,314 * 130 J = 9158,32827 J ≈ 9,158 KJ
Suche nach V3, gegeben ist V2 und T2 und T3
Bei p = const. gilt:
$$\frac{V_{3}}{V_{2}} = \frac{T_{3}}{T_{2}} = \frac{430\cdot K}{300\cdot K} \approx 1,433$$
V3 = 1,433 * V2 = 1,433 * 0,024746 m3 = 0,035461018 m3 ≈ 0,035461 m3
Zustand 4
C) isochor in den Zustand IV (TIV = 350 K), V = const.
T3 = 430 K und T4 = 350 K, ΔT = T4 - T3 = (350 -430 ) K = - 80 K, Abkühlung ΔT < 0
V4 = V3
Das System kühlt bei konst. Volumen ab, gibt Wärme an das Wärmebad(Kühlbad. Umgebung) ab. Der Druck nimmt ab. Die Innere Energie nimmt auch ab, weil das System Wärme an die Umgebung abgibt.
Bei Volumenkonstanz also ΔU statt &DeltaH, es wird keine Volumarbeit mit der Umgebung ausgetauscht.
ΔU = n * Cv,m * ΔT
Jetzt muß man mit der molaren Wärmekapazität bei konst. Volumen rechnen.
Wie lautet nun die molare Wärmekapazität bei konst. Volumen für 2 atomige perfekte Gase?
Die Volumarbeit fehlt(R), aber es sind 3 Translationsfreiheitsgrade(3/2 R) plus 2 Rotationsfreiheitsgrade (2 / 2 R) vorhanden, also es sind dann ohne die Schwingungsfreiheitsgrade, die erst bei höheren Temperaturen auftreten, in der Summe 5 / 2 R.
$$C_{v,m} = \frac{5}{2}\cdot R$$
$$\Delta U = n\cdot \frac{5}{2}\cdot R\cdot \Delta T$$
$$\Delta U = 2,421\cdot mol\cdot \frac{5}{2}\cdot \frac{8,314\cdot J}{K\cdot mol}\cdot ( - 80\cdot K)$$
ΔU = ( - 80 ) * 2,421 * 2,5 * 8,314 J = - 4025,6388 J ≈ - 4,026 KJ
Zustand 4, Der Druck p4 und die Partialdrücke von Stickstoff, p4(N2) und Sauerstoff, p4(O2) über die gegebenen Stoffmengenanteile, x(N2) = 0,8 und x(O2) = 0,2
T4 = 350 K und V4 = V3 = 0,035461 m3
$$p_{4} = \frac{n\cdot RT_{4}}{V_{3}}$$
$$p_{4} = \frac{2,421\cdot 8,314\cdot Nm\cdot 350\cdot K}{K\cdot mol\cdot 0,035461 m^{3}}$$
$$p_{4} \approx 198665,235 \cdot \frac{N}{m^{2}} \approx 198.665 Pa = 1,98665 bar$$
Nach der Daltonbeziehung gilt für die Partialdrücke der Komponenten der idealen Gasmischung:
p4(N2) = x(N2) * p4, und
p4(O2) = x(O2) * p4
p4(N2) = 0,8 * 1,98665 bar = 1,58932 bar ≈ 1,59 bar
p4(O2) = 0,2 * 1,98665 bar = 0,39733 bar ≈ 0,397 bar
Zu den Partialdichten aus den Partialdrücken im Zustand 4 , ρ4(N2) und ρ4(O2)
Es gilt:
$$p = \frac{n\cdot RT}{V} = \frac{m}{M}\cdot \frac{RT}{V} = \frac{m}{V}\cdot \frac{RT}{M}$$
$$p = \varrho \cdot \frac{RT}{M}$$
$$p_{4}(N_{2}) = \varrho _{4}(N_{2}) \cdot \frac{RT}{M(N_{2})}$$
$$p_{4}(O_{2}) = \varrho _{4}(O_{2}) \cdot \frac{RT}{M(O_{2})}$$
mit :
$$\varrho _{4}(N_{2}) = p_{4}(N_{2})\cdot \frac{M(N_{2})}{RT}$$
bzw.
$$\varrho _{4}(O_{2}) = p_{4}(O_{2})\cdot \frac{M(O_{2})}{RT}$$
Molmassen, ganzzahlig gerundet:
M(O2) = 32 g / mol und M(N2) = 28 g / mol
$$\varrho _{4}(N_{2}) = \frac{ 158.932\cdot N}{m^{2}}\cdot \frac{28\cdot g\cdot K\cdot mol}{mol\cdot 8,314\cdot Nm\cdot 350\cdot K}$$
$$\varrho _{4}(N_{2}) = \frac{1529,295\cdot g}{m^{3}} \approx 1,529 \cdot \frac{g}{l} = 1,529 \cdot \frac{mg}{ml}$$
$$\varrho _{4}(O_{2}) = \frac{ 39733\cdot N}{m^{2}}\cdot \frac{32\cdot g\cdot K\cdot mol}{mol\cdot 8,314\cdot Nm\cdot 350\cdot K}$$
$$\varrho _{4}(O_{2}) = 436,942\cdot \frac{g}{m^{3}} = 0,436942\cdot \frac{g}{l} = 0,436942\cdot \frac{mg}{ml}$$
Tragen Sie die Zustandsänderungen in ein p-V-Diagramm ein. Berechnen Sie die Partialdrücke
pi und die Partialdichten ρi der Komponenten im Zustand IV und die reversible Volumenarbeit
wrev für den Prozess A.
Skizze