Grüße chemweazle,
Die Volumenarbeit eines Systems
Aufgabe: Beim Befüllen eines Schutzgastankes werden 40 mol Argon aus einer 5 L Transportflasche (interner Druck 200 bar) zunächst bei konstanten 100 bar in die Leitung und in einem zweiten Schritt in bei konstanten 20 bar in den Tank überführt.
a) Veranschaulichen Sie diesen Prozess anhand eines entsprechenden pV-Diagramms und berechnen Sie die Volumenarbeit.
b) Wie ändert sich die Volumenarbeit, wenn der Prozess reversibel durchgeführt wird?
Zeichnen Sie auch zu diesem Prozess das entsprechende pV-Diagramm.
Gehen Sie bei Ihren Berechnungen von idealem Verhalten des Argons aus.
Die Diagramme befinden sich am Ende diese Beitrags .
Das Produkt von Druck und Volumen ist const. nach Robert Boyle, bei fester Stoffmenge n und gegebener, konstanter Temperatur, n = const. und T = const.
p * V = nRT = const, = p1 * V = 1 = p2 * V = 2 = p3 * V3, etc.
Mit p1 * V1 = p2 * V2 = const., gilt auch :
$$\dfrac{p_{1}}{p_{2}} = \dfrac{V_{2}}{V_{1}}$$
Das Volumenverhältnis ist umgekehrt dem Verhältnis der beiden Drücke und umgekhert entspricht da Verhältnis zweier Drücke dem umgekehrten Volumenverhältnis.
Expandiert ein perfektes Gas bei const. Temperatur von einem höheren Anfangsdruck, pA mit einem kleineren Anfangsvolumen, VA gegen einen niedrigeren Druck, Enddruck, pE unter Volumenvergrößerung auf das Endvolumen VE, mit VE > VA, so gilt :
$$\dfrac{V_{E}}{V_{A}} = \dfrac{p_{A}}{p_{E}}$$
$$V_{E} = V_{A} \cdot \dfrac{p_{A}}{p_{E}}$$
Für die Volumarbeit im Fall der irreversiblen Expansion des idealen Gases gegen den kleineren Enddruck, pE,gilt :
$$w = - p_{E}\Delta V = - p_{E}\cdot ( V_{E} – V_{A} )$$
Mit dem Volumenverhältnis ist gleich dem umgekehrten Verhätnis der beiden Drücke kann man auch für die Volumendifferenz, Δ V = VE - VA schreiben :
$$\Delta V = V_{E} – V_{A} = V_{A} \cdot \dfrac{p_{A}}{p_{E}} - V_{A} = \left(\dfrac{p_{A}}{p_{E}} - 1 \right)\cdot V_{A}$$
$$w = - p_{E}\cdot V_{A}\cdot \left(\dfrac{p_{A}}{p_{E}} - 1 \right)$$
Für die Volumarbeit im Fall der reversiblen Expansion des idealen Gases gilt :
$$w = - nRT\int \limits_{V_{A}}^{V_{E}}\frac{dV}{V}$$
$$w = - nRT\cdot ln\left(\dfrac{V_{E}}{V_{A}}\right)$$
oder
$$w = - nRT\cdot ln\left(\dfrac{p_{A}}{p_{E}}\right)$$
Die isotherme Expansion des perfekten Gases erfolgt beginnend vom höchsten Anfangsdruck, pA = 200 bar in 2 Schritten gegen einen kleineren Druck, pE = 100 bar und dem geringsten der 3 Drücke, dem Enddruck, pE = 20 bar.
1. Isothermer Expansionsschritt von pA = 200 bar nach pE = 100 bar = 0,5 * pA
Bei den Bedingungen: T0 = 298,16 K und pA = 200 bar = 2 * 107 N / m2 nehmen n = 40 mol Argon folgendes Volumen ein :
$$V_{A} = \dfrac{nRT}{p_{A}} = \dfrac{40\cdot mol\cdot 8,314\cdot Nm\cdot 298,16\cdot K\cdot m^{2}}{K\cdot mol\cdot 2\cdot 10^{7}\cdot N}$$
VA ≈ 0,00496 m3 = 4,96 l , das sind gerundet 5 l, wie in der Aufgabenstellung angegeben.
$$nRT = \dfrac{40\cdot mol\cdot 8,314\cdot Nm\cdot 298,16\cdot K\cdot m^{2}}{K\cdot mol}$$
$$nRT \approx 99156,0896 Nm = 99156,0896 J$$
Das Volumenverhältnis nach und vor der 1. Expansion
$$\dfrac{V_{E}}{V_{A}} = \dfrac{p_{A}}{p_{E}} = \frac{200\cdot bar}{100\cdot bar} = 2$$
Das Endvolumen VE:
$$V_{E} = V_{A}\cdot \dfrac{p_{A}}{p_{E}}$$
$$V_{E} = 5\cdot l\cdot 2 = 10\cdot l$$
Halber Druck, doppeltes Volumen
Die Volumänderung, Δ V = VE - VA :
Δ V = VE - VA = ( 10 - 5 ) l = 5 l = 0,005 m3
a).Die Volumarbeit bei der irreversiblen, isothermen Expansion des Gases gegen den Enddruck von
pE = 100 bar = 107 N / m2
w = - pE Δ V = - pE * ( VE - VA )
$$w = - 0,005\cdot m^{3}\cdot \dfrac{10^{7}\cdot N}{m^{2}} = - 5\cdot 10^{-3+7}\cdot Nm = - 5\cdot 10^{4}\cdot J = - 50 KJ$$
b).Die Volumarbeit bei der reversiblen, isothermen Expansion des Gases gegen den Enddruck von pE = 100 bar = 107 N / m2
$$w = - nRT\int\limits_{V_{A}}^{V_{E}}\ \frac{dV}{V} = - nRT\cdot ln\left(\dfrac{V_{E}}{V_{A}}\right)$$
$$w = - nRT ln\left(\dfrac{p_{A}}{p_{E}}\right)$$
Mit
$$ln\left(\dfrac{p_{A}}{p_{E}}\right) = ln(2) \approx 0,6932 $$
und nRT = 99.156,09 J
$$w \approx - 99.156,0896\cdot J \cdot 0,691 \approx - 68735,001\cdot J \approx 68,735\cdot KJ$$
Zum Vergleich : w(irrev.) = - 5 * 104 J = - 50 KJ und w(rev.) = - 68,74 KJ
2. Expansionsschritt, isotherm
2. Schritt der isothermen Expansion gegen den kleineren Enddruck, von pE = 20 bar = 2 * 106 N / m2
Volumenverhältnis
$$\dfrac{V_{E}}{V_{A}} = \dfrac{p_{A}}{p_{E}} = \frac{100\cdot bar}{20\cdot bar} = 5$$
Das Endvolumen VE:
$$V_{E} = V_{A}\cdot \dfrac{p_{A}}{p_{E}} = 10\cdot l\cdot 5 = 50\cdot l = 0,05\cdot m^{3}$$
Bei einem Fünftel des vorherigen Drucks, das Fünffache an Volumen
Die Volumänderung, Δ V = VE - VA = ( 50 -10 ) l = 40 l = 0,04 m3
a).Die Volumarbeit bei der irreversiblen, isothermen Expansion des Gases gegen den Enddruck von pE = 20 bar = 2 * 106 N / m2
w = - pEΔ V = - pE * ( VE - VA )
$$w = - 0,04\cdot m^{3}\cdot \dfrac{2\cdot 10^{6}\cdot N}{m^{2}} = - 8\cdot 10^{-2+6}\cdot Nm = 8\cdot 10^{4}\cdot J = - 80\cdot KJ$$
b).Die Volumarbeit bei der reversiblen, isothermen Expansion des Gases gegen den Enddruck von pE = 20 bar = 2 * 106 N / m2
$$w = - nRT ln\left(\dfrac{p_{A}}{p_{E}}\right) = - 99.156,0896 J \cdot ln(5) \approx - 99.156,0896 J\cdot 1,60944$$
$$w \approx - 159,586 KJ$$
Zum Vergleich : w(irrev.) = - 80 KJ und w(rev.) = - 159,586 KJ
Bei der idealen reversiblen Prozeßführung wird mehr Arbeit an die Umgebung verrichtet, abgegeben.
Schritt 1 Volumenverdopplung, Druckhalbierung
w(irrev.) = - 50 KJ und w(rev.) = - 68,74 KJ
Schritt 2 Fünftelung des Drucks, isotherm, Verfünffachung des Ausgangsvolumens
Zum Vergleich : w(irrev.) = - 80 KJ und w(rev.) = - 159,586 KJ
_____________________________________________________________________
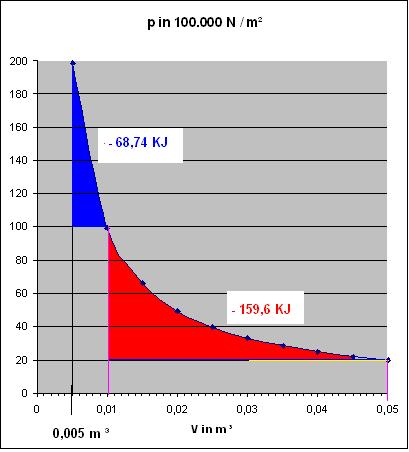
Zu den Diagrammen, Nr.1 Für die beiden irreversiblen, isothermen Expansionen und Nr. 2 Für die beiden reversiblen Expansionen
In beiden Diagrammen ist die Hyperbel-Kurve des Drucks, p = nRT/V blau eingezeichnet.
Die Berechnung der Kurve ergibt sich aus:
$$p = \frac{nRT}{V} = \frac{99.156,0896\cdot Nm}{V}$$
Das Volumen in Kubikmeter. Die Werte der Drücke wurden für die Volumina im Intervall von 0,005 m3 bis 0,05 m3 in 0,005 m3- Schritten berechnet.
Die Diagramme wurde mit Excel und nachher mit MS-Paint bearbeitet.
Skizze Isotherme, irreversible Expansionen
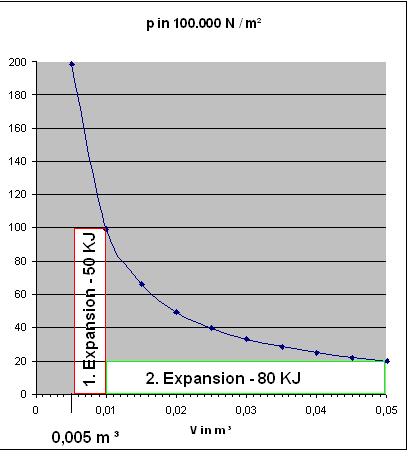
Skizze Isotherme, reversible Expansionen