Grüße chemweazle,
Titration Schwefelsäure: Berechnung der pH-Werte der Äquivalenzpunkte
Aufgabe: Es werden 100 mL einer verd. Schwefelsäure unbekannter Konzentration mit NaOH (c=0,1 mol/L) titriert. Als Indikator dient Phenolphtalein. Bis zum Umschlagpunkt des Indikators werden 20 mL NaOH verbraucht.
a) Berechne die Konzentration der Schwefelsäure.
b) Zeichne den Verlauf der Titrationskurve. Wie viele Äquivalenzpunkte weist die Titrationskurve auf und bei welchen pH-Werten werden diese gefunden?
Problem/Ansatz: Bei der a) war ich mir eigentlich sicher mit meiner Lösung. Die b) hat mich dann aber an der Lösung für a) zweifeln lassen. Daher habe ich auch die a) mal hier mitangegeben.
zu a):
H2SO4 + 2 NaOH -> Na2SO4 + 2 H2O
n(NaOH)= c*V=0,02 mol -> n(H2SO4)= 0,5* n(NaOH)= 0,01 mol
c(H2SO4)= n/V= 0,08 mol/L
Der Rechenweg stimmt schon, nur die Stoffmengen an zugegebener NaOH und verbrauchter Schwefelsäure sind um den Faktor 10 zu hoch.
Konz. der Maßlösung : c(NaOH) = 0,1 mol / l = 0,1 mmol / ml und das Volumen der Maßlösung : V(NaOH) = 20 ml = 0,02 l
n(NaOH) = c(NaOH) * V(NaOH) = [ 0,1 mol / l ] * 0,02 l = 0,1 * 0,02 mol = 0,002 mol = 2 mmol
$$\dfrac{n(H_{2}SO_{4})}{n(NaOH)} = \frac{1}{2}$$
$$n(H_{2}SO_{4}) = \frac{1}{2}\cdot n(NaOH) = 0,5\cdot 0,002\cdot mol = 0,001\cdot mol = 1\cdot mmol$$
Das Aliquotvolumen, V(Aliquot), der Analysenlösung mit der verd. Schwefelsäure beträgt 100 ml = 0,1 l.
$$c(H_{2}SO_{4}) = \dfrac{n(H_{2}SO_{4})}{V(Aliquot)}$$
$$= \frac{0,01\cdot mol}{l}$$
• Bis zum Umschlag des Indikators(Phenolphtalein) ist der 2. Äquivalenzpunkt erreicht.
Beim Umschlag von Phenolphtalein ist also die Schwefelsäure vollständig zu Natrimsulfat titriert worden.
Stichwort : Volltitration
Am 2. ÄP liegt dann, wie auch schon in der Reaktionsgleichung richtig wiedergegeben, eine reine Natriumsulfatlösung(Na2SO4) vor.
jetzt zur b): Kurve weiß ich und es müssen zwei Äquivalenzpunkte sein.
Das stimmt.
Am Anfang vor der Zugabe der Zugabe der Maßlösung(NaOH-Lsg.) liegt die verd. Schwefelsäurelösung vor.
Die Schwefelsäure ist in ihrer Erstdissoziation eine starke Säure und liegt vollständig in Hydroniumionen und Hydrogensulfationen dissoziiert vor.
Erstdissoziation, vollständig, da starke Säure
H2SO4 → H(+)(aq) + HSO4(-)(aq)
Das heißt es liegen überhaupt keine undissoziierten H2SO4 - Moleküle vor.
Die Hydrogensulfationen sind eine mittelstarke Säure und liegen nur zum Teil in Hydroniumionen und Sulfationen dissoziiert vor.(pKs = 1,97)
HSO4(-)(aq) ⇌ H(+)(aq) + SO4(2-)(aq)
Die Titration vom Anfangspunkt, reine Verd. Schwefelsäure-Lsg. bis zum 1. ÄP ist die Titration einer starken Säure mit einer starken Base.
Beim 1. Äquivalenzpunkt liegt eine reine Natrium-Hydrogensufatlösung(Halbtitration) vor.
Wenn die Hälfte der Maßlösung zugegeben wurde, ist die Schwefelsäure zum Natriumhydrogensulfat (mittelstarke Säure) umgesetzt worden.
Es befanden sich im Aliquot von 100 ml eine Stoffmenge von 1 mmol an Schwefelsäure.
Aus dieser enstand bei der Halbtitration 1 mmol = 0,001 mol Natriumhydrogensulfat.
Diese ist eine mittelstarke Säure. Der pKs-Wert beträgt, pKs(HSO4(-)) = 1,97.
pH- Wert, Hydroniumionenkonzentration und die Ausgangs-Konzentration an Hydrogensulfat
Bis zur Erzeugung der reinen Natriumhydrogensulfat-Lsg. ist die Hälfte an Maßlösung zugegeben worden, es sind 10 ml an NaOH-Maßlösung.
Das Mischvolumen, VMix, beträgt, V mix = V(Aliquot) + V(NaOH) = 100 ml + 10 ml = 110 ml = 0,11 l.
Die Ausgangskonzentration an Natriumhydrogensulfat
Stoffmenge an Natriumhydrogensulfat bzw. Hydrogensulfationen
n(NaHSO4) = n(HSO4(-)) = 0,001 mol = 1 mmol
Anfangs-Konzentration an Hydrogensulfationen im Mischvolumen bei der Halbtitration, VMix = 110 ml = 0,11 l
$$c0(HSO_{4}^{(-)}) = \dfrac{n(HSO_{4}^{(-)})}{VMix} = \frac{0,001\cdot mol}{0,11\cdot l} = \frac{0,1}{11}\cdot \frac{mol}{l} = \frac{1}{110}\cdot \frac{mol}{l} \approx 0,0091\cdot \frac{mol}{l}$$
Die Näherungsformel zu Berechnung der Hydroniumionen-Konzentration bei der Dissoziation verdünnter schwacher Säuren, gilt auch angenähert für mittelstarke Säuren.
$$[H^{(+)}] = \sqrt{Ks\cdot c0}$$
oder in der logarithmierten Form
$$pH = \frac{pKs}{2} - \dfrac{log_{10}(|c0|)}{2}$$
$$pH \approx \frac{1,97}{2} - \dfrac{lg_{10}(0,0091)}{2} \approx 0,985 - -1,021 = 0,985 + 1,021 \approx 2,01\approx 2$$
Zwischen den beiden Äquivalenzpunkten, dem 1. ÄP und dem 2. ÄP, befindet sich der sogenannte Pufferbereich mit den Hydrogensulfationen als konjugierte Säure und den Sulfationen als konjugierte Base.
Die pH-Werte zwischen den beiden Äquivalenzpunkten lassen sich mit der Henderson-Hasselbalch-Gleichung errechnen. Die Henderson-Hasselbalch-Gleichung gilt nicht für die beiden Äquivalenzpunkte selbst.
$$pH = pKs(HSO_{4}^{(-)}) + log_{10}\left(\dfrac{c(SO_{4}^{(2-)})}{c(HSO_{4}^{(-)})}\right)$$
Denn beim 1. ÄP liegt die Dissoziation einer mittelstarken Säure, Hydrogensulfat, vor.
Beim 2. ÄP hingegen müßte man die Basenreaktion der Sulfationen erwarten, sicherlich sehr schwach ausgeprägt, da der pKb-Wert der Sulfationen ca. 12 beträgt.
2. ÄP, erwartete Basenreaktion der Sulfationen, Ausgangs-Konzentration der Sulfationen, (Volltitration)
Das Mischvolumen ist das Aliquotvolumen plus die 20 ml Maßlösung der 0,1 m NaOH-Lsg.
VMix = V(Aliquot) + V(NaOH) = 100 ml + 20 ml = 120 ml = 0,12 l
Stoffmenge an Sulfationen, n0(SO4(2-))
Aus 0,001 mol Hydrogensufationen sind nun 0,001 mol Sulfationen durch die Säure-Base-Reaktion mit den Hydroxidionen der Maßlösung entstanden.
HSO4(-)(aq) + OH(-)(aq) → SO4(2-)(aq) + H2O
$$c0(SO_{4}^{(2-)}) = \dfrac{n(SO_{4}^{(2-)})}{VMix} = \frac{0,001\cdot mol}{0,12\cdot l} \approx 0,0083\cdot \frac{mol}{l}$$
Basenreaktion der Sulfationen, wenn auch sehr schwach
SO4(2-)(aq) + H2O ⇌ HSO4(-)(aq) + OH(-)(aq)
$$pOH \approx \dfrac{pKb(SO_{4}^{(2-)})}{2} - log_{10}(|c0(SO_{4}^{(2-)})|)$$
Der pKb-Wert der Sulfationen ergibt sich aus : 14 - pKs(HSO4(-))
pKb(SO4(2-)) = 14 - pKs(HSO4(-)) = 14 - 1,97 = 12,03
$$pOH \approx \frac{12,03}{2} - \dfrac{log_{10}(0,0083)}{2} = 6,015 - - 1,0396 \approx 6,02 + 1,04 = 7,06$$
pH = 14 - pOH = 14 - 7,06 = 6,94 ≈ 7, neutrale Lösung
Die Basenreaktion der Sulfationen ist vernachlässigbar .
Äquivalenzpunkte 1 und 2 deren pH-Werte
ÄP 1 , pH1 = 2,01 und ÄP 2, pH2 = 6,94 ≈ 7
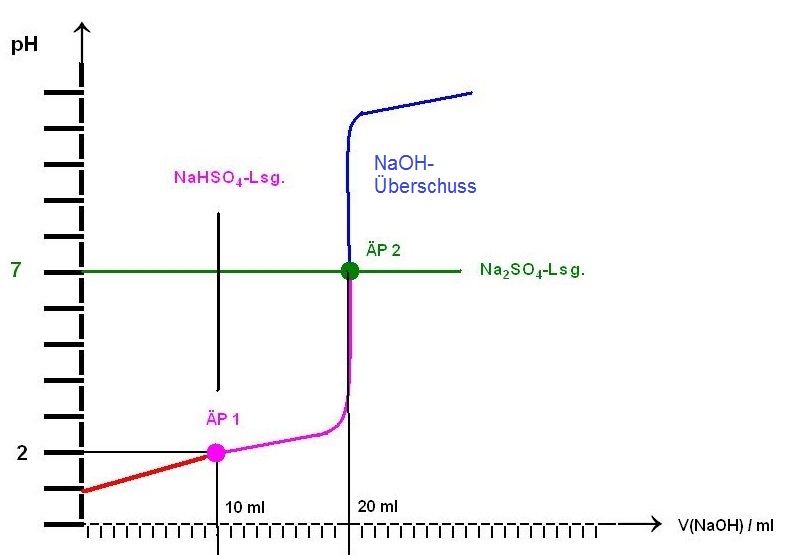
Skizze der Titrationskurve zur Titrat. von Schwefelsäure mit NaOH-Lsg.
http://daten.didaktikchemie.uni-bayreuth.de/experimente/chembox/phlf_h2so4/phlf_h2so4.htm