Berechnen Sie den pH-Wert und Wie ändert sich der pH-Wert

Question

Aufgabe:

Eine Probe einer HCI-Lösung mit Einem Gemisch

Problem/Ansatz:

Eine Probe einer HCI-Lösung (c=0,10 mol/L. V = 10 mL) wird mit NaOH (c=0,10 mol/L)
titriert.

a) Zeichnen Sie die Titrationskurve für diese Reaktion! Berechnen Sie dazu den pH-Wert
der Probe vor Zugabe von NaOH und den Verbrauch an NaOH bei Erreichen des
Aquivalenzpunktes!

b) Ein Gemisch aus Essigsäure und Natriumacetat (NaCH₂COO) ist ein häufig
verwendetes Puffersystem. Berechnen Sie den pH Wert des resultierenden Puffers
wenn zu verdünnter Essigsäure (0,060 mol in 250 mL Gesamtvolumen) 0,030 mol festes
Natriumacetat (NaCH,COO) gegeben werden! Die Volumenänderung durch die Zugabe
von Natriumacetat wird vernachlässigt.

c) Wie ändert sich der pH-Wert, wenn in dieser Lösung 0,005 mol Ba(OH)2 gelöst
werden? Auch hier wird die Volumenänderung als vernachlässigbar angenommen.

Comments

Hilfe bitte!

---

keine Hilfe hier ./

---

????? Hilfe bräuhte

Answer 1

Grüße chemweazle,

bin wieder viertelwegs genesen, deshalb so verspätet die Reaktion.

Zum Aufgabenblock

Berechnen Sie den pH-Wert und Wie ändert sich der pH-Wert

Aufgabe a). Titration einer verd. ,wäßr. HCl-Lösung
Aufgabe b). Herstellung eines HOAc-NaOAc-Puffers
Aufgabe c). Zugabe von Bariumhydroxid( 2säurige) starke Base
Eine Probe einer HCI-Lösung (c=0,10 mol/L. V = 10 mL) wird mit NaOH (c=0,10 mol/L)
titriert.

Aliquot:
Die zu titrierend wäßr. HCl-Lsg., Aliquot-Volumen, V(Aliquot) = 10 ml ,und c(HCl) = 0,1 mol / l = 0,1 mmol / ml

Maßlösung
0,1 m NaOH-Lsg. , c(NaOH) = 0,1 mol / l = 0,1 mmol / ml
a) Zeichnen Sie die Titrationskurve für diese Reaktion! Berechnen Sie dazu den pH-Wert
der Probe vor Zugabe von NaOH und den Verbrauch an NaOH bei Erreichen des
Aquivalenzpunktes!
____

Die Hydroniumionen-Konzentration und der pH-Wert der zu titrirenden Lsg, Aliquot , betragen:

c(H⁽⁺⁾) = c(HCl) = 0,1 mol / l = 10^-1 mol / l

pH = – log₁₀ ( c(H⁽⁺⁾) ) = – log₁₀ ( c(HCl) )

pH = – log₁₀ ( 10^-1 mol / l * l / mol ) = – – 1 = + 1

Titration bis zum Erreichen des Äquivalenzpunkts (Neutralpunkt)
Am Äquivalenzpunkt liegt eine neutrale NaCl-Lösung vor.

H⁽⁺⁾_(aq) + OH^(-)_(aq) → H₂O

Es wurde beim Erreichen des Äquivalenzpunkts die äquivalente , gleiche Stoffmenge an Hydroxidionen aus der Maßlöung hinzuggeben, wie Hydroniumionen, H⁽⁺⁾-Ionen, im Aliquotvolumen vorlagen.

n(H⁽⁺⁾)_verbraucht = n(HCl)_verbraucht = n(OH^(-))_hinzugegeben = n(NaOH)_hinzugegeben

n(H⁽⁺⁾)_verbraucht = n(HCl) = c(HCl) * V(Aliquot) = c(NaOH) * V(NaOH)

n(H⁽⁺⁾)_verbraucht = n(HCl) = c(HCl) * V(Aliquot) = 0,1 [ mol / l ] * 0,01 l = 0,001mol = 1 mmol

n(NaOH)_hinzugegeben = n(H⁽⁺⁾)_verbraucht = 0,001 mol = 1 mmol

$$V(NaOH) = \dfrac{n(NaOH}{c(NaOH)} = \dfrac{0,001\cdot mol\cdot l}{0,1\cdot mol}$$
$$V(NaOH) = \frac{0,001}{0,1}\cdot l =\frac{1}{1000}\cdot 10\cdot l = \frac{1}{100}\cdot l = 0,01\cdot l = 10 ml$$

Am Neutralpunkt(Endpunkt) ist die Hydroniumionen-Konzentration und der pH-Wert nur noch durch die schwache, geringfügige Eigendissoziation des Wassers bestimmt.

Eigendissoziation des Wassers<7p>

H₂O → H⁽⁺⁾_(aq) + OH^(-)_(aq)

Bei der Temperatur von 25 °C sind 10^-7 mol / l der Wasser-Moleküle in 10^-7 mol / l H⁽⁺⁾-Ionen und 10^-7 mol / l Hydroxidionen dissoziert.

Das Ionenprodukt, bei θ = 25 °C, lautet: Kw = c(H⁽⁺⁾) * c(OH^(-)) = 10^-14 mol² * l^-2

c(H⁽⁺⁾) = c(OH^(-)) = 10^-7 mol / l

pH = 7 = pOH

Skizze der Titrationskurve, rot : saurer Bereich, grüner Punkt: Äquivalenzpunkt, blau: NaOH-Überschuß-Teil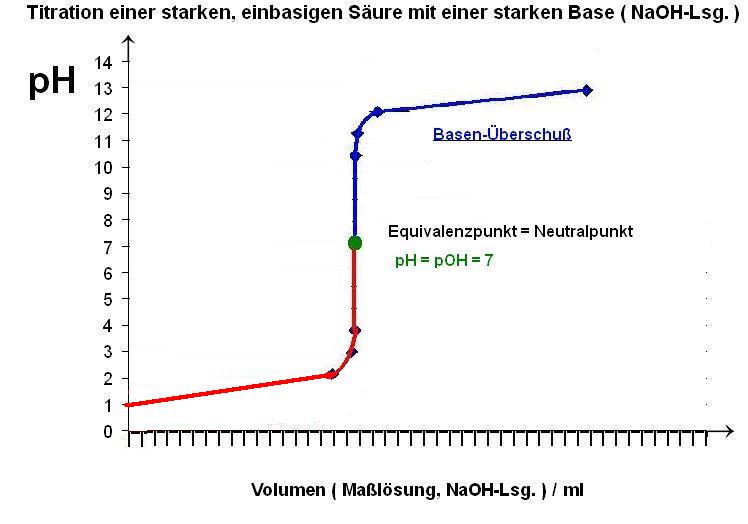

Aufgabe b)., HOAc-AcO^(-)-Puffer

b) Ein Gemisch aus Essigsäure und Natriumacetat (NaCH₃COO) ist ein häufig verwendetes Puffersystem. Berechnen Sie den pH Wert des resultierenden Puffers wenn zu verdünnter Essigsäure (0,060 mol in 250 mL Gesamtvolumen) 0,030 mol festes Natriumacetat (NaCH₃COO) gegeben werden!

Die Volumenänderung durch die Zugabe von Natriumacetat wird vernachlässigt.

c) Wie ändert sich der pH-Wert, wenn in dieser Lösung 0,005 mol Ba(OH)₂ gelöst werden? Auch hier wird die Volumenänderung als vernachlässigbar angenommen.

Konjugierte Säure : Essigsäure, Ethansäure, HOOC-CH₃, Abkürzung : HOAc

Konjugierte Base: Acetation aus Natriumacetat, CH₃COO^(-) aus NaCH₃COO ; abgekürzt: mit AcO^{(-) und NaOAc}

Die Abkürzung Ac steht für den Acetyl-Rest, CH₃-CO-

Henderson-Hasselbalch-Gleichung

$$ pH = pKs(HOAc) + log_{10}\left[\dfrac{c(konjugierte Base) }{c(konjugierte Säure)}\right]$$

$$pH = pKs(HOAc) + log_{10}\left[\dfrac{c(^{(-)}OAc)}{c(HOAc)}\right]$$

Anmerkung : Das Konzentrationsverhältnis ist auch gleich das Stoffmengen-Verhältnis.
Im Bruchterm des Konzentrationsverhältnisses kürzt sich das Volumen der Puffergemisch-Lösung, V , heraus.
$$\dfrac{c(^{(-)}OAc)}{c(HOAc)} = \dfrac{n(^{(-)}OAc)\cdot V}{n(HOAc)\cdot V}$$
Oder man kann den Bruchterm auch mit dem Faktor 1 = [ V / V ] erweitern.
$$\dfrac{c(^{(-)}OAc)}{c(HOAc)} = \dfrac{c(^{(-)}OAc)}{c(HOAc)}\cdot \frac{V}{V} = \dfrac{n(^{(-)}OAc)}{n(HOAc)}$$

Konzentrationen

Konjugierte Säure, HOAc : c(HOAc) = 0,06 mol / 0,25 l = 0,24 mol / l

Konjugierte Base, NaOAc, c(NaOAc) =c (AcO^(-) ) = 0,03 mol / 0,25 l = 0,12 mol / l

$$\dfrac{c(^{(-)}OAc)}{c(HOAc)} = \dfrac{n(^{(-)}OAc)}{n(HOAc)} = \frac{0,03\cdot mol\cdot 0,25\cdot l}{0,25\cdot l0,06\cdot mol} = \frac{1}{2} = 0,5$$
$$pH = 4,75 + log_{10}\left(\frac{1}{2}\right)$$

pH = 4,75 + log₁₀(1) – log₁₀(2)

pH = 4,75 + 0 – log₁₀(2)

pH ≈ 4,7500 – 0,3010 = 4,449 ≈ 4,45

Zu c).

Zugabe der starken 2-säurigen, 2-wertigen Base, wasserfreies Bariumhydroxid, Ba(OH)₂

Zugabe der starken 2-säurigen, 2-wertigen Base, wasserfreies Bariumhydroxid, Ba(OH)₂

Setzt man z.B. eine 1 molare Bariumhydroxid-Lsg. an, so sind in einem Volumen von einem Liter 1 mol hydratisierte Barium(II)-Kationen aber 2 mol Hydroxidionen gelöst.

n(OH^(-)) = 2 * n(Ba⁽²⁺⁾) und c(OH^(-)) = 2 * c(Ba⁽²⁺⁾)

0,005 mol Bariumhydroxid liefert gelöst 0,005 mol Barium(II)-Ionen und die doppelte Stoffmenge an OH^(-)-Ionen, also 2 * 0,005 mol = 0,01 mol.

Dem oben erwähnten Essigsäure-Acetat-Puffergemisch wurden nun insgesamt 0,01 mol Hydroxidionen zugegeben.

Jedes OH^(-)-Ion reagiert mit einem 1 HOAc-Molekül zu einem Wassermolekül und dabei wird ein zusätzliches Acetation erzeugt.

0,01 mol OH^(-)-Ionen fangen 0,01 mol Essigsäure ab und die Stoffmenge der Acetationen erhöht sich um 0,01 mol, dabei nimmt die Stoffmenge an Essigsäure um 0,01 mol ab.

HOAc_(aq) + OH^(-)_(aq) ⇌ AcO^(-)_(aq) + H₂O

Stoffmengen an HOAc und Acetat in dem Viertel Liter ( V = 0,25 l ) vor der Zugbe an Bariumhydroxid

n(HOAc) = 0,06 mol und n(AcO^(-)) = 0,03 mol

Stoffmengen an HOAc und Acetat in dem Viertel Liter nach der Zugabe von 0,01 mol OH^(-)-Ionen aus 0,005 mol Bariumhydroxid

n(HOAc) = 0,06 mol – 0,01 mol = 0,05 mol

n(AcO^(-)) = 0,03 mol + 0,01 mol = 0,04 mol

Die neuen Konzentrationen an HOAc und Acetat im Viertel Liter (0,25 l) Gemischvolumen
$$c(HOAc) = \dfrac{0,05\cdot mol}{0,25\cdot l} = 0,2\cdot \frac{mol}{l}$$
$$c(AcO^{(-)}) = \dfrac{0,04\cdot mol}{0,25\cdot l} = 0,16\cdot \frac{mol}{l}$$
$$\dfrac{c(AcO^{(-)})}{c(HOAc)} = \dfrac{n(AcO^{(-)})}{n(HOAc)} = \frac{0,04\cdot mol}{0,05\cdot mol} = \frac{4}{5} = \frac{8}{10}$$

pH = 4,75 + log₁₀(0,8) ≈ 4,75 – 0,097 ≈ 4,653 ≈ 4,65