// Bitte Frage nicht löschen , KEIN CROSS-POSTING, Wurde gelöscht auf anderer Plattform Gelöscht!!!! Frage Wurde gelöscht auf anderer Plattform ///
Hallo liebe Leute,
ich habe Probleme bei dieser Aufgabe. Sie ist sehr groß. Ich hoffe auf eure Hilfe. Vielen Dank im voraus . Ich bin nur bis d) gekommen und hier bin ich mir nicht sicher, ob meine Rechnungen richtig sind.
Ein Hörsaal \( ^{1} \) hat die Abmessungen \( L=12 \mathrm{m}, B=8 \mathrm{m}, H=3 \mathrm{m} . \) Der Sauerstoffgehalt der Luft beträgt \( x_{O_{2}}=0.20, \) der initiale \( C O_{2} \) -Gehalt entspricht \( x_{C O_{2}}=400 \) ppm. Desweiteren sind die Raumbedingungen \( \vartheta=23^{\circ} \mathrm{C} \) und \( p=990 \) mbar. Der Hörsaal ist mit 50 hochinteressierten Studierenden und 1 Dozenten belegt. Alle anwesenden Personen haben pro Atemzug (Dauer \( \Delta t=6 \) s) ein durchschnittliches Lungenvolumen von \( V_{L}=0.5 \mathrm{L} \) unter Normbedingungen. Der Sauerstoffgehalt in der ausgeatmeten Luft hat sich um \( \Delta x_{O_{2}}=0.04 \) verringert. Der Stoffwechsel im Körper (pro Atemzug) erfolge vereinfachend gemäß folgender Reaktion (Zucker \( \left.=C_{6} H_{12} O_{6}\right): \)
Zucker + Sauerstoff \( \longrightarrow \) Kohlendioxid \( + \) Wasser
(a) Fertigen Sie eine Skizze des beschriebenen Systems an, das den Prozess , Atmen " darstellt sowie die dabei auftretenden (relevanten) Stoffe enthält.
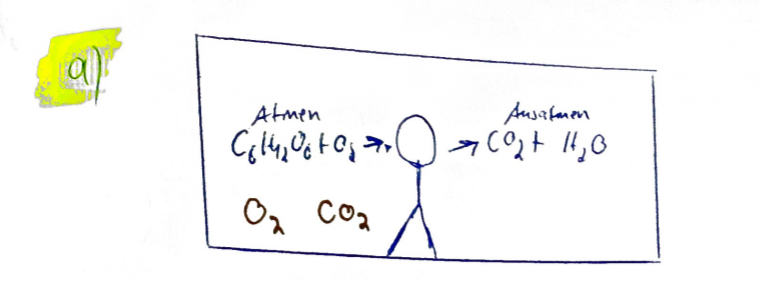
Text erkannt:
\( a\rangle \)
(b) Stellen Sie die Reaktionsgleichung in Formelschreibweise inkl. der ausgleichenden stöchiometrischen Koeffizienten auf. Berechnen Sie vor Beginn der Vorlesung \( (t=0 \mathrm{h}) \) für \( \mathrm{O}_{2} \) und \( \mathrm{CO}_{2} \ldots \)
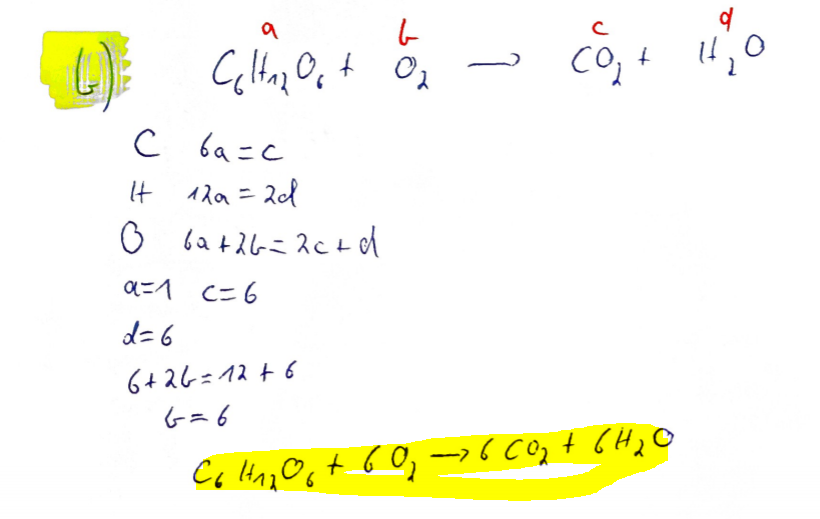
Text erkannt:
1
5
\( C \quad 6 a=c \)
\( 1+\quad 12 a=2 d \)
\( 0 \quad 6 a+2 c=2 c+d \)
\( a=1 \quad c=6 \)
\( d=6 \)
\( 6+26=12+6 \)
\( 5=6 \)
\( c_{6} 1+10_{6}+60,-76 \mathrm{co}_{2}+6420 \)
(c) \( \ldots \) die Partialdrücke \( p_{i} \) gemäB der Gleichung \( p_{i}=p \cdot x_{i} \) (Gesetz von DALTON).
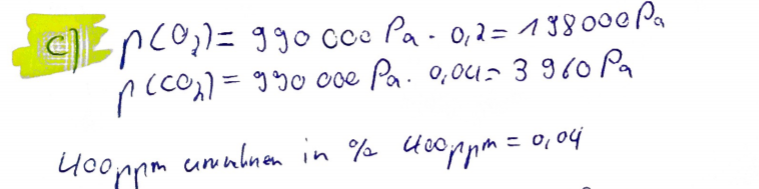
Text erkannt:
C) \( 13 \mathrm{r}(0,9)=990 \mathrm{cco} \mathrm{Pa} \cdot 0,2=19800 \mathrm{OPa} \)
\( n(c 0,)=930000 P_{a} \cdot 0,04=3960 \mathrm{Pa} \)
Uoonnm unulinen in \( \% \) laonpm \( =0,04 \)
(d) \( \ldots \) die Stoffmengenkonzentrationen \( c_{i} \) in der Raumluft in \( \left[\frac{m o l}{m^{3}}\right] \).
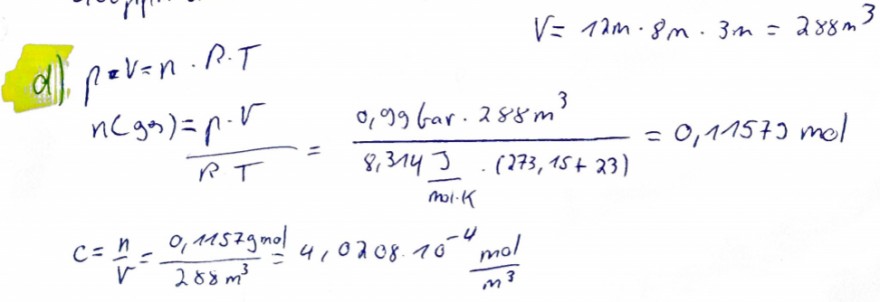
Text erkannt:
\( V=12 m \cdot 8 \mathrm{m} \cdot 3 \mathrm{m}=288 \mathrm{m}^{3} \)
\( x \|_{1} p_{x} v=n \cdot R \cdot T \)
\( c=\frac{n}{V}=\frac{0,11579 \mathrm{mol}}{288 \mathrm{m}^{3}}=4,0208 \cdot 10^{-4} \frac{\mathrm{mol}}{\mathrm{m}^{3}} \)
(e) \( \ldots \) die insgesamt vorliegenden Stoffmengen \( n_{i} \) beider Komponenten im Raum.
(f) \( \ldots \) die Stoffmenge \( \Delta n_{O_{2}} \), die pro Person und Atemzug verbraucht wird. \( ^{2} \) Berechnen Sie nach einer Stunde \( (t=1 \mathrm{h}) \ldots \)
(g) ... die Anzahl an Atemzügen, die innerhalb der Stunde von allen Anwesenden insgesamt getätigt werden.
(h) ... die Stoffmengen an Sauerstoff und Kohlendioxid in [mol] sowie die Masse an Zucker in [g], die von allen Beteiligten in dieser Zeit verbraucht bzw. erzeugt wurden.
(i) ... die Stoffmengen von \( \mathrm{O}_{2} \) und \( \mathrm{CO}_{2} \), die nun im Raum vorhanden sind. \( ^{3} \)
(j) \( \ldots \) die aktuellen Konzentrationen von \( \mathrm{O}_{2} \) und \( \mathrm{CO}_{2} \)
(k) Recherchieren Sie mit Quellenangabe einen MAK-Wert \( ^{4} \) von \( C O_{2} \) und kommentieren Sie damit ihr berechnetes Ergebnis aus der vorigen Teilaufgabe.
Hinweise: GemäB dem Gesetz von Dalton setzt sich der Druck eines Gases aus der Summe der Partialdrücke zusammen: \( \sum\left(p_{i}\right)=p \)