Gruß chemweazle,
Zur
Titration von Aminosäuren mit starken Säuren
Berechnung Aminosäuregehalt über Titration
Du hast ein Fläschen mit 890mg einer Prolin-haltigen Probe bekommen. Hier von wurden 205 mg Probe abgewogen und anschließend laut Skript titriert. Es wurden 16 mL HBr-Maßlösung (0.1N) aus der Bürette zugetropft. Wie viel Prolin [in mg] war in dem gesamten Fläschen enthalten?
Prinzip
Die Zwitterionen von Aminosäuren haben noch eine schwach basische, anionische Carboxylatgruppe(-CO2(-)).
Diese Zwitterionen können an den schwach basischen Carboxylgruppen noch von starken Säuren, wie z.B.: wäßrige Lösungen von HCl, HBr und Perchlorsäure, protoniert werden.
Es entstehen dabei die "protonierten Zwitterionen", die aci-Form der Zwitterionen, diese sind Kationen und haben als Gegenion(Anion) das Anion der eingesetzten Säure, bei HCl das Chloridion usw.
Beispiel mit Glycin
H3N(+)—CH2—CO2(-)(aq) + H(+)(aq) + Cl(-)(aq) → H3N(+)—CH2—CO2H(aq) + Cl(-)(aq)
Säure-Base-Titration(Titration der α-Aminosäure Prolin) mit wäßriger HBr-Maßlösung
Skizze
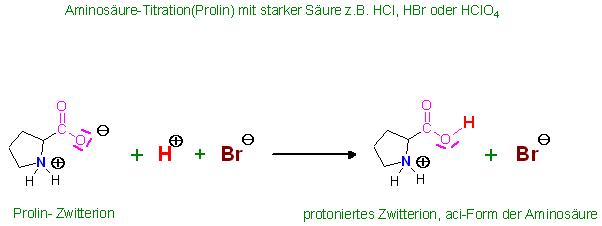
Stöchiometrie
1 mol Aminosäure fängt 1 mol Protonen auf. Diese stammen aus 1 mol HBr.
n(Prolin) = n(H(+)) = n(HBr)
n(Prolin) = n(H(+)) = n(HBr) = c(HBr-Lsg.) * V(HBr-Lsg.)
Mit c(HBr-Lsg.) = 0,1 mol / l = 0,1 mmol / ml und dem Maßlösungsvolumen von V(HBr-Lsg.) = 16 ml, ergibt sich für die Stoffmenge an Prolin in der Probe:
n(Prolin) = c(HBr-Lsg.) * V(HBr-Lsg.) = ( 0,1 mmol / ml ) * 16 ml = 1,6 mmol
In der Probe mit der Masse von m(Probe) = 205 mg, liegt eine Stoffmenge von 1,6 mmol an Prolin vor.
Aus der Stoffmenge an Prolin, n(Prolin) und der zugehörigen Molmasse, M(Prolin), läßt sich die Masse an Prolin in der Probe berechnen und der Massenanteil an Prolin, w(Prolin), in der Probenmasse.
Molmasse von Prolin
Bruttoformel: C5H9NO2
M(C5H9NO2) = (12,011*5+1,0079*9+14,0067*+15,9994*2) g / mol = 115,1316 g / mol
m(Prolin) = n(Prolin) * M(Prolin)
$$m(Prolin) = 1,6\cdot mmol\cdot \frac{115,1316\cdot mg}{mmol} = 184,21056\cdot mg\approx 184,211\cdot mg$$
$$w(Prolin) = \frac{m(Prolin)}{m(Probe)} = \frac{184,211\cdot mg}{205\cdot mg} \approx 0,8986 = 89,86\%$$
Der Massenanteil, w(Prolin), an Prolin in der Probe beträgt in etwa 0,8986, entsprechend 89,86 %.
Der Massenanteil in der Probe ist identisch mit dem Massenanteil der Pulvergemisches in dem Fläschchen.
Im "Fläschchen" befand sich eine Gesamtmasse von 890 mg an prolinhaltigem Gemisch.
Die Masse an Prolin in diesem Gemisch ist Massenanteil mal der Gesamtmasse dieser Mischung.
Also: m(Prolin im Fläschlein) = w(Prolin) * m(Gemisch im Fläschlein) = 0,8986 * 890 mg = 799,754 mg