Gruß chemweazle,
Die maximal mögliche Größe der Br( -) -Ionen
LiBr kristallisiert in der dichtesten kubischen Kugelpackung. Berechnen Sie aus dem
Gitterparameter die maximal mögliche Größe der Br-
-Ionen und vergleichen Sie diesen Wert
mit dem Tabellenwert. Kommt es durch die Li+
-Ionen zu einer Aufweitung der Struktur?
Gitterparameter a(LiBr)=550pm
Gitterparameter a(LiBr)=550pm, Gitterkonstante, kubisches System
LiBr kristallisiert in der NaCl-Struktur. D.h. es liegen eine kubisch-dichteste, kubisch-flächenzentrierte Packung der Bromidionen und eine kubisch-flächzentrierte Kugelpacnkung der Lithiumionen vor.
Das Anionenteilgitter ist kubisch-flächenzentriert und das Kationen-Teilgitter ist kubisch-flächenzentriert.
Das Kationenteilgitter ist so in das Anionenteilgitter geschoben, daß die Lithiumionen alle Oktaeder-lücken ausfüllen.
Eine Würfelkante, a, der Elementarzelle des NaCl-Gitters setzt sich aus der Summe der Radien, wie folgt zusammen.
a = r(Br(-)) + 2 * r(Li(+)) + r(Br(-))
a = 2 * r(Li(+)) + 2 * r(Br(-))
Die Flächendiagonale, d, aus einem Elementarzellen-Ausschnitt beträgt das Quadratwurzel aus 2-fache der Kantenlänge, Gitterkonstanten, a, mit :
$$d = \sqrt{2}\cdot a$$
Die Flächendiagonale ist auch 4mal dem Anionenradius der Bromidionen, d = 4 * r(Br(-))
$$d = \sqrt{2}\cdot a = 4\cdot r(Br^{(-)})$$
$$\Rightarrow r(Br^{(-)}) = \dfrac{\sqrt{2}}{4}\cdot a$$
$$r(Br^{(-)}) = \dfrac{\sqrt{2}}{4}\cdot 550\cdot pm$$
$$r(Br^{(-)})\approx \frac{1,414}{4}\cdot 550\cdot pm$$
$$r(Br^{(-)})\approx 194,425\cdot pm$$
___________________________________
Lithium-Ionenradius
mit: a = 2 * r(Li(+)) + 2 * r(Br(-))
2 * r(Li(+)) = a - 2 * r(Br(-))
$$r(Li^{(+)}) = \frac{a}{2} - r(Br^{(-)})$$
$$r(Li^{(+)}) = \frac{550\cdot pm}{2} - 194,425\cdot pm$$
$$r(Li^{(+)}) = (275 - 194,425)\cdot pm = 80,575\cdot pm$$
Skizze
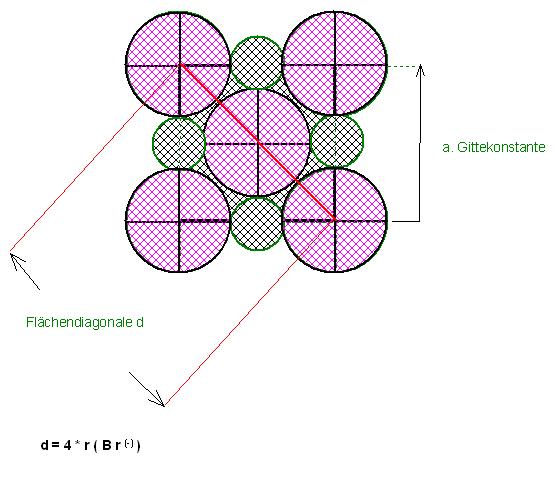
___________________________________
zum Vergleich
Ionenradien nach Shannon, für die Koordinationszahl 6, basierend auf r(O(2-)) = 140 pm
r(Br(-)) = 196 pm und r(Li(+)) = 76 pm
entnommen aus:
U. Müller, Anorganische Strukturchemie, 3., überarb. u. erw. Aufl., Stuttgart; Teubner, (1996), Seite 48-49, Kap. 5.4 Ionenradien
Eine geringfügige Aufweitung bzgl. der Lithiumionen, deren Radius um ca. 4 pm größer erscheint.
Das Ionenradiusverhältnis wäre nach dem Hartkugel-Modell, für den Quotienten Anionenradius zu Kationenradius,
r(K(+)) /r(A(-)) = 0,414 = ( 1,414 - 1 )
$$\frac{r(K^{(+)})}{r(A^{(-)})} = \sqrt{2} - 1 \approx 1,414 - 1 = 0,414$$
$$\dfrac{r(Br^{(-)})}{r(Li^{(+)})} = \frac{80,575}{194,425} \approx 0,4144\approx 0,415$$
Das Radiusverhältnis Kation zu Anion stimmt ziemlich gut mit der Hartkugel-Näherung überein.
Keine großartigen Aufweitungen im Kristallgitter.
