Grüße chemweazle,
Molare Verdampfungsenthalpie mithilfe der Clausius-Clapeyron-Gleichung ermitteln (Auftragung)
Die folgenden Dampfdrücke wurden in Abhängigkeit der Temperatur für Salpetersäure gemessen.
T in *C
0 20 40 50 70 80 90 100
p in mbar 19,2 63,9 177 277 623 893 1249 1700
Die August´sche auch Antoine´sche Dampfdruck-Formel hergeleitet aus der Clausius-Claperyon´schen Gleichung
$$ln\left(\dfrac{p_{2}}{p_{1}}\right) = \dfrac{\Delta _{verd.}H_{m}}{R}\cdot \left(\dfrac{1}{T_{1}} - \dfrac{1}{T_{2}}\right)$$
$$\blue{ln\left(\dfrac{p_{2}}{p_{1}}\right)} = \green{\dfrac{\Delta _{verd.}H_{m}}{R}}\cdot \red {\left(\dfrac{T_{2} - T_{1}}{T_{1}\cdot T_{2}}\right)}$$
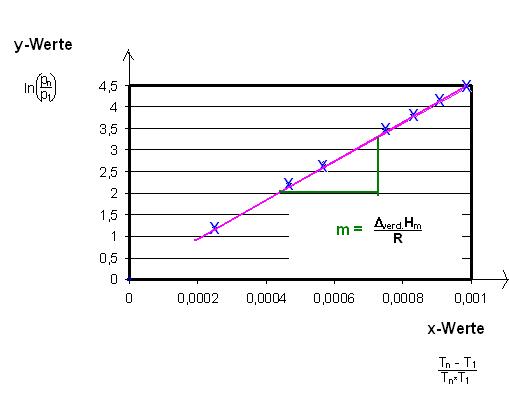
y = m * x
Die Steigung der Geraden multipliziert mit R ergibt nun die Molare Verdampfungs-Enthalpie.
Vorgehensweise
Man trage die 8 Werte-Paare von ln(p8 / p1) mit T8 - T1 / T8 * T1 , ln(p7 / p1) mit T7 - T1 / T7 * T1 , ln(p6 / p1) mit T6 - T1 / T6 * T1 , usw. bis einschließlich ln(p1 / p1) mit T1 - T1 / T1 * T1 in ein Diagramm auf.
Die Meßpunkte(Wertepaare) liegen auf einer Geraden.
Die Steigung, m, der Geraden ist die Molare Verdampfungsenthalpie geteilt durch die Gaskonstante R .
Steigung der Geraden m
$$m = \frac{\Delta y}{\Delta x} = \dfrac{\Delta _{verd.}H_{m}}{R}$$
Die Steigung der Geraden multipliziert mit R ergibt nun die Molare Verdampfungs-Enthalpie.
Diese Gerade geht durch den Nullpunkt, Ursprung des Koordinatensystems.
Denn der erste y-Wert, y1 = 0 = ln(p1 / p1) = ln(1) = 0
Ebenfalls ist der 1. x-Wert auch Null. x1 = (T1 - T1) / (T1 * T1) = 0.
Berechnung der y-Werte
Bildung der Druckverhältnisse und den natürlichen Logarithmen aus den Druckverhältnissen
Zunächst kann man jeden der 8 Drücke, p8 bis p1 durch den kleinsten Wert, p1 dividieren.
Dann kann man die natürlichen Logarithmen aus den 8 Druckverhältnissen bilden, das sind auch schon die Funktionswerte(y-Werte), die auf die Ordinate( y-Achse ) aufgetragen werden.
| Temperatur in °C | Absolute Temperatur in K | Druck p in mbar |
| 0 | 273,16 | 19,2 |
| 20 | 293,16 | 63,9 |
| 40 | 313,16 | 177 |
| 50 | 323,16 | 277 |
| 70 | 343,16 | 623 |
| 80 | 353,16 | 893 |
| 90 | 363,16 | 1249 |
| 100 | 373,16 | 1700 |
| Druck p in mbar | $$\dfrac{p_{n}}{p_{1}}$$ | $$ln\left(\dfrac{p_{n}}{p_{1}}\right)$$ |
| 19,2 | 1 | 0 |
| 63,9 | 3,328125 | 1,20240908 |
| 177 | 9,21875 | 2,22123945 |
| 277 | 14,4270833 | 2,66910723 |
| 623 | 32,4479167 | 3,47963624 |
| 893 | 46,5104167 | 3,8396763 |
| 1249 | 65,0520833 | 4,17518823 |
| 1700 | 88,5416667 | 4,48347325 |
Berechnung der 8 x-Werte, x1 bis x8
$$x_{n} = \dfrac{T_{n} – T_{1}}{T_{n}\cdot T_{1}}$$
Beispiel$$x_{1} = \dfrac{T_{1} – T_{1}}{T_{1}\cdot T_{1}} = 0$$
$$x_{4} = \dfrac{T_{4} – T_{1}}{T_{4}\cdot T_{1}}$$
Man bilde Differenzen indem man von jedem der 8 Temperaturwerte den kleinsten Temperaturwert, T1 subtrahiert.
Differenzen: T8 - T1 , T7 -T1, ...., T2 - T1 und T1 - T1
Ebenso kann man die Produkte der Temperaturen als Zwischenwerte verwenden.
Jeder der 8 Temperatuwerte wird mit dem kleinsten Temperaturwert multipliziert.
T8 * T1 , T7 * T1, .... bis T2 * T1 und T1* T1
| T / in K | Temperatur-Differenz Tn – T1 in K | Produkte Tn * T1 in K2 |
| 273,16 | 0 | 74616,3856 |
| 293,16 | 20 | 80079,5856 |
| 313,16 | 40 | 85542,7856 |
| 343,16 | 50 | 88274,3856 |
| 343,16 | 70 | 93737,5856 |
| 353,16 | 80 | 96469,1856 |
| 363,16 | 90 | 99200,7856 |
| 373,16 | 100 | 101932,386 |
| X-WERTE | Y-WERTE |
| $$x_{n} = \dfrac{T_{n} – T_{1}}{T_{n}\cdot T_{1}}$$ | $$ln\left(\dfrac{p_{n}}{p_{1}}\right)$$ |
| 0 | 0 |
| 0,00024975 | 1,20240908 |
| 0,0004676 | 2,22123945 |
| 0,00056642 | 2,66910723 |
| 0,00074677 | 3,47963624 |
| 0,00082928 | 3,8396763 |
| 0,00090725 | 4,17518823 |
| 0,00098104 | 4,48347325 |
Die durch die Lineare Regression , Ausgleichsrechnung, ermittelte Steigung lautet:
$$m = \dfrac{\sum y_{i}\cdot x_{i} - \sum y_{i}\cdot \sum x_{i}}{\sum x_{i}^{2} - \left[\sum x_{i}\right]^{2}}$$
Steigung, m = 4566,79166
Die Molare Verdampfungsenthalpie
Δverd.Hm = R * m ≈ 8,314 J K-1 mol-1 * 4566,79166 = 37968,30586 J K-1 mol-1
Skizze